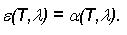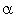|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
||
| Startseite | Artikel | Smilies | Projekte | Computer | Fotoalbum | Hobbies | Fun | Links | Gästebuch | Impressum | Sitemap | Linktausch |
Du bist zur Zeit hier: Startseite / Projekte /
Thermosäule
|
Thema: berührungslose Temperaturmessung mit der Thermosäule Inhaltsverzeichnis
Nummerierung und Verweise:
Die Nummerierung der Bilder, Tabellen, Gleichungen und Literatur gilt für das jeweilige Kapitel. Gleichungs-, Grafiknummern und Literaturziffern stehen in runden ( ) Klammern. Außerdem in der Fußnote und im Quellenverzeichnis. 1. Einleitung
In dieser Facharbeit werden, auf den folgenden Seiten, Methoden zur berührungslosen Temperaturmessung und deren Erfinder ausführlich beschrieben. Daher werden zu Beginn dieser Facharbeit einige der bedeutendsten Wissenschaftler vorgestellt, die sich mit dem Thema der Wärmeabstrahlung und der dazugehörigen Messung beschäftigt haben. Da das Thema aber sehr weitreichend ist, wird sich weitestgehend an die Quellen im Literaturverzeichnis gehalten.
Thomas Johann Seebeck
Max Planck
Josef Stefan
Durch Messungen zeigte er 1879, dass sich die Strahlung eines schwarzen Körpers proportional zur vierten Potenz der Temperatur verhält. Ludwig Boltzmann, einer seiner Studenten, gab 1884 den mathematischen Beweis für das Stefan-Boltzmann-Gesetz. Um die Temperatur auf der Sonnenoberfläche zu bestimmen, wandte Stefan dieses Gesetz an. Außerdem arbeitete er an der Wärmeleitung in Fluiden und der kinetischen Wärmetheorie. Josef Stefan starb am 7. Januar 1893 in Wien.
Ludwig Boltzmann
2. Versuche2.1 Berührungslose Temperaturmessung mit dem Leslie-Würfel
Abbildung 2.1.1 
Als erstes wird in einen Würfel ca. 40°C warmes Wasser eingefüllt. Dieser sogenannte Leslie-Würfel besteht aus Blech und hat vier verschiedene Oberflächen - eine schwarze und eine weiße Seite, als auch eine matte u[1]nd eine polierte bzw. spiegelnde Metalloberfläche. Mit der oben dargestellten Thermosäule wird die Wärmestrahlung, die der Leslie-Würfel abgibt, gemessen. Zunächst misst man die Oberflächentemperatur mit dem elektrischen Digitalthermometer. Diese ergibt für die schwarze zu messende Oberfläche 38,8°C. Nun werden der Reihe nach die einzelnen Oberflächen mit dem Infrarot-Thermometer abgetastet und die Temperatur gemessen. Für die schwarze Fläche erhält man einen Wert von 38,0°C. Der Wert der weißen Fläche liegt etwas darüber, nämlich bei 38,2°C. Einen deutlichen Unterschied dazu erkennt man aber bei der matten bzw. verspiegelten Oberfläche. Hier pendeln sich die Werte bei 29,1°C bzw. 29,0°C ein. Dies lässt sich dadurch erklären, dass die verschiedenen Oberfläche jeweils einen anderen Emissionsgrad besitzen. Bei lackierten (schwarz, weiß) Oberflächen beträgt er ca. 0,6 - 0,9, bei blanken jedoch nur 0,05 - 0,1. Eine weitere Auffälligkeit besteht darin, dass sich die mit dem Infrarot-Thermometer (Abbildung 2.1.2) gemessene Temperatur verändert, wenn man den Winkel zwischen dem Thermometer und dem Würfel verkleinert bzw. vergrößert. Dies lässt sich mit dem Richtungsgesetz von Lambert erklären, näheres dazu in Kapitel 3.3.5.
Abbildung 2.1.2
Temperaturmessgerät
durch Infrarotstrahlung (21) 2.2 Messungen mit der Thermosäule
Zunächst einmal füllt man den Leslie-Würfel bis zum oberen Rand mit Leitungswasser. Man hängt das elektrische Thermometer ins Wasser und misst die Temperatur. Die anfängliche Wärme beträgt 20.4 °C. Nun stellt man den Würfel auf einen kleinen Holzblock, damit die Thermosäule besser zum Leslie-Würfel ausgerichtet werden kann. Die mit dem Spannungsmessgerät verbundene Thermosäule bringt man, im Abstand von 1 cm, an den Würfel heran (siehe Abbildung 2.2.1). Bei der oben gemessenen Temperatur des Wassers sollte das Voltmeter (siehe Abbildung 2.2.2) einen Wert von 0 mV anzeigen, wenn nicht, wird es darauf justiert.
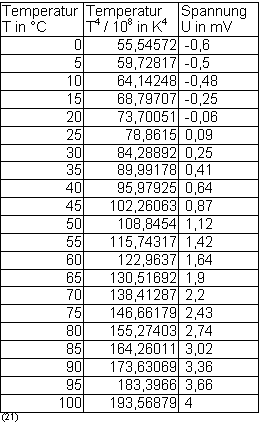
Dann zerschlägt man den Eisblock in mehrere kleine Brocken und gibt diese dem Wasser hinzu. Jetzt wird im Abstand von 5°C jeweils die Temperatur der schwarzen Oberfläche des Leslie-Würfels, als auch die angezeigte Spannung der Thermosäule in einer Tabelle zusammengefasst. Der erste Messpunkt liegt etwas unter der Anfangstemperatur des Wassers, nämlich bei 20 °C. Diese Messungen führt man durch bis der Wert 0°C erreicht ist. Der daraufhin in das Wasser gehängte Wasserkocher soll dieses dann auf eine Temperatur von ca. 100 °C erwärmen. Knapp unter 100° deshalb, weil das Wasser sonst anfängt zu verdampfen und zu sprudeln, wodurch es überkochen kann. Während dieser Erwärmungsphase nimmt man, wie vorher, im Abstand von 5°C, die Temperatur und die dazugehörige Spannung. Wenn die Temperatur 100°C beträgt, wird der Wasserkocher entnommen. Das erwärmte Wasser wird nun wieder abgekühlt und die beiden Werte werden nochmals bei den gleichen Temperaturen abgelesen und in eine separate Tabelle eingetragen. Vergleicht man die Werte der Erwärmungsphase mit denen der Abkühlungsphase, stellt man fest, dass sie nicht gleich sind. Im Durchschnitt sind die Spannungswerte in der Erwärmungsphase um 0,1 bis 0,2 mV größer als die Werte in der Abkühlungsphase. Dies lässt sich dadurch erklären, dass der Würfel die Temperatur des Wassers schneller aufnimmt, als er sie wieder abgibt, was schon Newton in seinem Newton’schen Abkühlungsgesetz erkannt hat. Schließlich werden die Werte Temperatur und Spannung in ein Diagramm eingetragen. Die selben Daten werden in ein zweites Diagramm übergetragen, nur wird die Temperatur zunächst in Kelvin umgerechnet und dieser Wert dann hoch 4 genommen. Anschleißend wird noch mal mit dem Faktor 108 dividiert, um die Werte besser ablesen zu können. Dieser Versuch gibt die Möglichkeit die Stefan-Boltzmann-Gleichung zu bestätigen, da in dieser Gleichung die Temperatur in T4 angegeben ist. (siehe Kapitel 3.5)
Abbildung 2.2.1
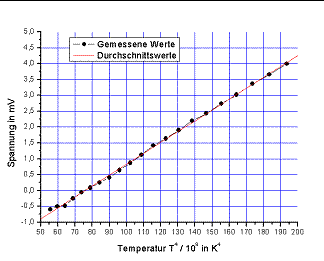
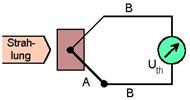
Die nachfolgende Abbildung zeigt den gesamten Aufbau der Versuchsanordnung (21): 3. Erklärung zu vorhergehenden Versuchen3.1 ThermoelementIm Jahr 1821 entdeckte Thomas Johann Seebeck den, nach ihm benannten, Seebeck-Effekt und konstruierte kurz darauf das erste Thermoelement.Im Grunde ist ein Thermoelement nur aus zwei Leitern aufgebaut, die miteinander verlötet sind. Der dabei entstehende Seebeck-Effekt lässt sich wie folgt erklären: Eine elektrische Spannung entsteht zwischen zwei Halbleitern, wenn diese unterschiedliche Temperaturen haben. Allerdings sind zwei verschiedene Metalle zu verwenden, denn nur dann treten Elektronen über, weil im anderen Metall möglicherweise eine energetisch bessere Bedingung herrscht. Durch diesen Elektronenfluss entsteht eine elektrische Spannung. Man nennt diese Spannung auch Thermospannung , welche nur einige Millivolt beträgt. (1) (9) Sie ist also abhängig von der Temperatur eines Kontakts. Bringt man nun eine der Kontaktstellen auf eine genau bestimmbare Temperatur, muss die andere nur noch auf die zu messende Temperatur erwärmt bzw. abgekühlt werden und die Elektronen werden regelrecht von einem Material zum anderen gedrückt. Hat man die Thermospannung ermittelt, kann man daraus auf die Temperaturdifferenz der beiden Kontaktstellen und damit auf die zu messende Temperatur schließen. Die Thermospannung besitzt ein positives Vorzeichen, wenn der Strom von der kälteren zur wärmeren Kontaktstelle fließt. Grundlage für den Seebeck-Effekt ist also der Einfluss des Temperaturunterschieds auf die Ladungsträger, die sich dann neu ordnen. Ist der Stromkreis geschlossen, fließt der sogenannte Thermostrom. Schaltet man viele solcher Kontaktstellenpaare hintereinander in Reihe, erhält man einfach messbare Ergebnisse. Diese Aneinanderreihung von Thermoelementen nennt man dann Thermosäule (siehe Kapitel 3.2), bei der sich die einzelnen Kontaktspannungen addieren. Zusätzlich wird ein Spannungsmessgerät in Serie geschaltet.
Es lässt sich aber auch eine negative Thermospannung erzeugen, wenn man einen sehr kalten Gegenstand vor die Kontaktstelle hält, wie schon im Versuch 2.2 durchgeführt. Dies entsteht dadurch, dass die Stellen zunächst weniger Strahlung absorbieren, als sie emittieren (11). Näheres dazu siehe Kapitel 3.6. Dadurch könnte aber der falsche Eindruck einer "Kältestrahlung" entstehen, welche es in diesem Zusammenhang nicht gibt. Da es keine verzögerungsfreien Regelkreise gibt, müssen geringfügige Temperatur-schwankungen hingenommen werden, wenn man die Temperatur der Vergleichsstelle mit einem Thermometer nimmt. Daher wird eine elektronische Variante eines Thermometers benutzt, um der Vergleichsstelle einen thermodynamischen Fixpunkt aufzuprägen und um jene Temperaturänderungen zu kompensieren.
Die Thermospannung lässt sich aber auch mathematisch ausdrücken: Die beiden Austrittsarbeiten WA1 und WA2 der verschiedenen Metalle lassen sich zu der Kontaktspannung U = WA1 + WA2 addieren (WA1 und WA2 sind elektrische Potentiale). Da WA1 und WA2 temperaturabhängig sind, ist folglich auch die Kontaktspannung temperaturabhängig, was aus dem auf Seite 10 oben beschriebenen Seebeck-Effekt folgt. Die Kontaktspannung gibt aber nur Temperaturunterschiede an, nicht jedoch den absoluten Wert. Besitzen die Kontakte nur geringfügig unterschiedliche Temperaturen, so treten einige Probleme mit der Temperaturbestimmung auf. (12)
Thermisch besonders günstige Materialien für die Kontaktstellenpaare (1):
Wichtig bei der Wahl der Materialien sind folgende Eigenschaften: · linearer Verlauf der Spannung über den Temperaturbereich · hohe Empfindlichkeit · hohe mechanische Belastbarkeit · Korrosions- und Alterungsbeständigkeit
3.2 Die ThermosäuleBei einer Thermosäule sind mehrere Thermoelemente hintereinander geschaltet. Thermosäulen werden hauptsächlich zur Messung im Infrarotbereich genutzt, wobei es heutzutage aber auch Ausführungen gibt, die auch im UV-Bereich verwendet werden können. Im Gegensatz zu pyroelektrischen Sensoren, hier ändert sich in Abhängigkeit von der aufgenommenen Wärme der Gitterabstand der Kristallatome, kann auch statische Strahlung gemessen werden. Je nach Ausführung sind sie sehr empfindlich. Häufig ermöglichen integrierte Thermistoren (wärmeempfindliche Widerstände) die Kompensation der Umgebungs- bzw. Bauelementetemperatur (15).
Aufbau Thermosäule: 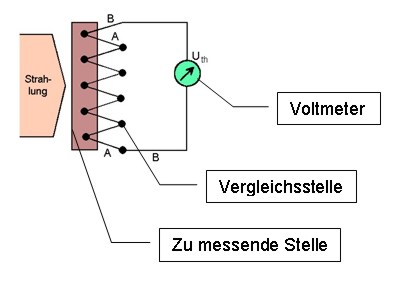
3.3 Hintergründe zur Thermospannung und zur berührungslosen Temperaturmessung3.3.1 Thermospannung Damit freie Elektronen aus einem der beiden Metalle abgelöst werden können, muss gegen die Anziehung der positiven Metallionen die Austrittsarbeit WA geleistet werden. Werden nun zwei Metalle mit verschiedener WA verlötet, fließen die Elektronen von dem Metall mit der kleineren Austrittsarbeit WA1 zu dem mit der größeren WA2. Durch die verschobenen Potentiale F, entsteht die Kontaktspannung U = F1 -F2, welche von der Temperatur des Kontakts abhängt. Für Elektronen im Metall gilt die Boltzmann-Verteilung (14):
n1 gibt die Teilchenkonzentrationen der Energie E1,n2 die von E2 wieder. Die Energieveränderung ist damit E1 - E2 Aus der Kontaktspannung U ist die Differenz der Elektronen-Austrittsarbeit gegeben: DE = - e(F2 -F1) = e U Löst man nun die Boltzmann-Verteilung nach ÇE auf, erhält man:
Der Quotient wird mehr durch die Austrittsarbeit WA als durch die Temperatur bestimmt. Zwischen zwei Kontakten, die unterschiedliche Temperaturen besitzen, entsteht somit eine Thermospannung Uth.
3.3.2 Wärmestrahlung Über dem absoluten Nullpunkt (-273°C) sendet jeder Körper elektromagnetische Wellen bzw. Strahlung ab. Im Bereich von 0,1 bis 1000 mm, also im Bereich des ultravioletten, sichtbaren und infraroten Lichts, wird diese als Wärmestrahlung bezeichnet. (3)
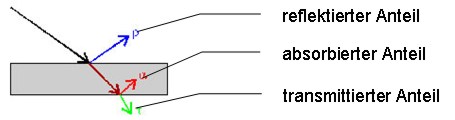
Die Strahlung, die auf einen Körper trifft, kann sowohl reflektiert (r), absorbiert (a), als auch durchgelassen bzw.
transmittiert (t) werden.
Dieses Verhalten wird von der Eigenschaft und der Oberfläche des bestrahlten Körpers beeinflusst. Die Anteile des jeweiligen Verhaltens addieren sich zu folgender Summe:
r + a + t = 1 Schwarze Strahler haben das größte Emissionsvermögen aller Oberflächen. Ihre Körpertemperatur wird in Strahlung umgewandelt. Ist das Emissionsvermögen einer Oberfläche kleiner 1 und unabhängig von Temperatur und Wellenlänge spricht man von einem grauen Strahler (6). Reale Oberflächen sind selektive Strahler.
3.3.4 Spezifische Ausstrahlung Reale Körper senden weniger Energie aus als der vergleichbare ideale schwarze Strahler. Man nennt diese dann graue Strahler. Die spektrale spezifische Ausstrahlung ål lässt sich aus der spezifischen Ausstrahlung eines schwarzen Strahlers å und dem Emissionsgrad el berechnen(16):
C1 und C2 sind Planck`sche Strahlungskonstanten:
C2 = 1,438·10-2 [in m·K]. Für einige Anwendungen ist die spezifische Ausstrahlung über alle Wellenlängen von Bedeutung:
e: Emissionsgrad
Allerdings gelten diese Formeln nur, wenn die Strahlung durch Vakuum hindurchgeht. Für alle andere Medien werden die beiden Formeln um die Brechzahl n erweitert.
3.3.6 Wien’sche Verschiebung (18) Die Strahlungsleistung, die den Körper verlässt, hat keine bestimmte Wellenlänge, sondern ist aus einem breiten Spektrum. Für jede Körpertemperatur ergibt sich eine bestimmte Strahlungskurve, welche von der Wellenlänge bestimmt wird. Bei einer steigenden Temperatur vergrößert sich die Strahlung und die maximal abgestrahlte Wellenlänge verkürzt sich. Bei genügend hoher Temperatur erstreckt sich die Kurve vom sichtbaren bis zum ultralangwelligen Spektralbereich. Bei niedrigen Temperaturen deckt die Kurve vorwiegend den langwelligen Spektralbereich ab.
Die Wellenlänge mit
der höchsten Intensität ist: T:
Temperatur des Strahlers in K 3.4 Die Planck’sche StrahlungsformelPlanck deutete im Jahr 1900, Licht in einem Hohlraum als ein Gas von Teilchen. Die einzelnen Gasatome besitzen unterschiedliche Bewegungsenergien, also sind sie unterschiedlich schnell. Je heißer nun ein Gas ist, desto schneller bewegen sich die Moleküle. Planck führte Lichtteilchen ein, die anstatt unterschiedlicher Geschwindig-keiten unterschiedliche Wellenlängen haben. Ein Teilchen von kurzwelligem Licht sollte mehr Energie haben, als eines von langwelligem Licht. Die Wellenlänge und die Energie drückte er durch eine Zahl, das sogenannte Planck’sche Wirkungsquantum, aus. Mit dieser Theorie kann die gemessene Strahlung exakt wiedergegeben werden. Die ausgesandte Strahlungsleistung eines Körpers ist abhängig von seiner Temperatur, deshalb wird sie auch spezifische Ausstrahlung genannt. Für die spezifische Ausstrahlung des schwarzen Körpers gilt nach Planck (2) (8) (19):
3.5 Gesetz von Stefan-BoltzmannDen Zusammenhang zwischen Strahlungsleistung und Wellenlänge beschreibt das Stefan-Boltzmann Gesetz für den idealen schwarzen Strahler:
Diese Formel bezeichnet man als die sogenannte Sigma T4-Formel. Sie wird aus der oben beschriebenen Planck`schen Strahlungsformel hergeleitet. Dies wird im folgenden geschehen.
Zunächst noch einmal die Planck’sche Strahlungsformel:
Um die Boltzmann-Gleichung zu
erhalten wird die obere Formel von der Grenze
=
Nun wird eine Substitution durchgeführt:
Durch diese Substitution haben sich aber auch die Grenzen verändert.
Setzt man Setzt man In Folge dieser Erkenntnis ist der Faktor –1 vor dem Integral notwendig, welcher sich aber wieder aufhebt, wenn man die Grenzen sofort wieder umdreht.
So erhält man folgende Formel:
Durch folgende Reihenentwicklung kann dieses Integral ausgerechnet werden:
Durch gliedweise Integrierung und Einführung der Integrationsvariable y = nx findet man:
Nutzt man nun die Definition der Gauß’schen Gammafunktion, die lautet: = x!, erhält man, für x = 3 und t = y folgenden Term:
Damit folgt:
Wie oben beschrieben ist der Bruch 3.6 Emission und Absorption3.6.1 Definition von Emissions- und Absorptionsvermögen Die Wärmestrahlung wird durch die abgestrahlte Leistung Peausgedrückt, doch wovon hängt Pe ab? Daher einige Erklärungen: Als Emissionsvermögen E bezeichnet man das Verhältnis der abgestrahlten Energie-menge eines Körpers zu der Menge, die von einem schwarzen Körper bei gleicher Temperaturbedingung abgestrahlt würde. (17)
Als Absorptionsvermögen
A bezeichnet man den für alle Wellenlängen gemittelten Quotienten, welcher
definiert ist als Körper, bei denen der Faktor A=1 ist, bezeichnet man als schwarze Körper. Von allen Körpern besitzt er das größte Emissionsvermögen.
Wie Experimente zeigen, ist Wärmestrahlung:
· reflektierbar. Im sichtbaren Bereich absorbiert ein dunkler Körper viel und reflektiert wenig, ein farbiger Körper absorbiert und reflektiert teilweise.
· absorbierbar, abhängig von Material und Dicke.
· abhängig vom betrachteten Frequenzbereich.
· abhängig von der Temperatur, Oberfläche und Oberflächenbeschaffenheit eines Körpers.
Aufgrund des letzten Punktes folgt eine kleine Abänderung des Stefan-Boltzmann-Gesetzes:
Auch der
Emissionsgrad Õ ist von der Oberflächenbeschaffenheit des Körpers abhängig und liegt
zwischen 0 und 1. Daraus folgt, dass e eine Funktion der Temperatur T und Wellenlänge l ist! Die ausgesandte und
aufgenommene Strahlungs-leistung ist somit temperatur- und
wellenlängenabhängig. Für alle Körper gilt (5)
Nachfolgend ist die Abhängigkeit zwischen dem Emissions- und Absorptionsvermögen beschrieben: Beide Körper
(hell und dunkel) besitzen die gleiche Temperatur, jedoch verschiedene
Oberflächen. Der Faktor
Falls Ist
Die Abkühlungsgeschwindigkeit eines Körpers ist näherungsweise proportional zur Temperaturdifferenz zwischen Körper und Umgebung. Diese Aussage bezeichnet man auch als das Newton'sche Abkühlungsgesetz.
3.6.2 Einflussfaktoren auf den Emissionsgrad Neben der bereits erwähnten Abhängigkeit des Emissionsgrads von der Wellenlänge und Temperatur, spielt das Material der Oberfläche und seine Beschaffenheit eine wichtige Rolle. Allgemein lässt sich sagen: blanke Metalle, wie sie in der Mikrosystemtechnik häufig vorkommen, haben einen sehr geringen, Kunststoffe einen sehr hohen Emissionsgrad. Eine "raue" Fläche (Oberflächenvergrößerung) führt ebenfalls zu einem höheren Emissionsgrad. 4. Anwendungen der Thermosäule und WärmestrahlungUm zu zeigen, dass sich die Funktionen der Thermosäule und die Wärmestrahlung auch in der Praxis Anwendung finden lassen, hier einige Beispiele:
5. Literaturverzeichnis
Textquellen: (1) http://pcitr4.fb10.tu-berlin.de/studium/lehre/scripte/tk1_skript.pdf, Stand 20.01.2004
(2) A. Frohn, Vorlesungsmanuskript Thermodynamik
III, Strahlung, (3) http://www.f1.fhtw-berlin.de/labor/adk/eua/scripte/pyrometrie, Stand 20.01.2004 (4) Bergmann-Schaefer, Lehrbuch der Experimentalphysik, Bd. 2, Elektromagnetismus, 8. Auflage, 1999, W. de Gruyter, Berlin (5) http://www.uni-stuttgart.de/itlr/forschung/infrarot.html, Stand 20.01.2004 (6) http://www.ebs-thermography.com/manual/emissions_g.html, Stand 22.01.2004 (7) http://www.harendt.de/studinf/pIII/quanten/plancksg.htm, Stand 20.01.2004 (8) http://klimt.iwr.uni-heidelberg.de/PublicFG/ProjectB/CFT/dipluschimpf/node5.html, Stand 20.01.2004 (9) http://www.net-lexikon.de/Seebeck-Effekt.html, Stand 23.01.2004
(10) http://www.ces.ka.bw.schule.de/lehrer/culm/messtechnik/sensoren/thermoelemente.htm
(11) http://www.hamburger-bildungsserver.de/welcome.phtml?unten=/klima/experimente/blk-ex1-522.html, Stand 20.01.2004 (12) http://www.pi1.physik.uni-stuttgart.de/Vorlesungsversuche/V626.html, Stand 20.01.2004 (13) http://www.minic.ac.at/ammu/17/17_7.htm, Stand 15.01.2004
(14) http://www.physik.uni-wuerzburg.de/physikonline/thermodynamik/g/sg09.html,
(15) http://www.sander-electronic.de/be00011.html, Stand 13.01.2004
(16) http://www.isd.uni-stuttgart.de/~buschbeck/sfb259B7/diplomarbeit_gerald/node9.html,
(17) http://www.physik.uni-wuerzburg.de/video/thermodynamik/t/st12.html, Stand 20.01.2004
(18) http://www.thermotemp.de/irtechnik.htm -
Wienersches%20Verschiebungsgesetz,
(19) http://www.quantenwelt.de/quantenmechanik/historisch/schwarze_korper.html,
(20) http://www.unibw-muenchen.de/campus/ETTI/we1/uhlmann/AP_Strahl_03.pdf,
(21) Neumann Benjamin, Stand 15.12.2003 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2004 - 2007 ·
· Aktualisiert am:
16.06.2007
|
 Thomas Johann
Seebeck wurde am 9. April 1770 in Reval (Tallin) geboren. Er machte eine
medizinische Ausbildung an den Universitäten von Berlin und Göttingen. Sein
Examen als Arzt legte er 1802 ab und praktizierte anschließend in Göttingen.
Jedoch entschied er sich in die physikalische Forschung zu wechseln. Deshalb
ist er heute als Physiker besser bekannt. Bevor er 1821 den thermoelektrischen
Effekt entdeckte, untersuchte er die Wärmewirkung unterschiedlicher Farben des
Solarspektrums. Seebeck veröffentlichte seine thermomagnetischen Arbeiten und
stellte 1823 eine thermoelektrische Spannungsreihe auf. Bevor er am 10.
Dezember 1831 starb, wirkte er 13 Jahre lang an der Berliner Akademie der
Wissenschaften.
Thomas Johann
Seebeck wurde am 9. April 1770 in Reval (Tallin) geboren. Er machte eine
medizinische Ausbildung an den Universitäten von Berlin und Göttingen. Sein
Examen als Arzt legte er 1802 ab und praktizierte anschließend in Göttingen.
Jedoch entschied er sich in die physikalische Forschung zu wechseln. Deshalb
ist er heute als Physiker besser bekannt. Bevor er 1821 den thermoelektrischen
Effekt entdeckte, untersuchte er die Wärmewirkung unterschiedlicher Farben des
Solarspektrums. Seebeck veröffentlichte seine thermomagnetischen Arbeiten und
stellte 1823 eine thermoelektrische Spannungsreihe auf. Bevor er am 10.
Dezember 1831 starb, wirkte er 13 Jahre lang an der Berliner Akademie der
Wissenschaften. Max Planck wurde am
23.04.1858 in Kiel geboren. Als deutscher Physiker revolutionierte er 1900 mit
seiner Quantentheorie das physikalische Weltbild. Er untersuchte neben der
Wechselwirkung von Atomen, Molekülen und Elementarteilchen, auch ob die
elektro-magnetische Energie eines schwarzen Körpers von seiner Temperatur und
der Frequenz der Strahlung abhängt. Im Jahr 1918 erhielt er den
Physik-Nobelpreis. Er starb am 04.10.1947 in Göttingen.
Max Planck wurde am
23.04.1858 in Kiel geboren. Als deutscher Physiker revolutionierte er 1900 mit
seiner Quantentheorie das physikalische Weltbild. Er untersuchte neben der
Wechselwirkung von Atomen, Molekülen und Elementarteilchen, auch ob die
elektro-magnetische Energie eines schwarzen Körpers von seiner Temperatur und
der Frequenz der Strahlung abhängt. Im Jahr 1918 erhielt er den
Physik-Nobelpreis. Er starb am 04.10.1947 in Göttingen. Josef Stefan wurde
am 24. März 1835 in der Nähe von Klagenfurt geboren. Er hielt Vorlesungen über
mathematische Physik in Wien und wurde 1858 Professor und Leiter des
physikalischen Instituts.
Josef Stefan wurde
am 24. März 1835 in der Nähe von Klagenfurt geboren. Er hielt Vorlesungen über
mathematische Physik in Wien und wurde 1858 Professor und Leiter des
physikalischen Instituts.  Ludwig Boltzmann wurde am 20. Februar 1844 in Wien
geboren. Er studierte Physik an der Universität Wien und war zwei Jahre
Assistent von Josef Stefan. 1869 wurde er Professor für mathematische Physik an
der Universität Graz. Das zentrale Problem seiner Arbeit war die Rückführung
der Thermodynamik auf die Mechanik und die dabei nötige Beseitigung des
Widerspruchs zwischen der Umkehrbarkeit mechanischer Vorgänge und der Einseitigkeit
thermodynamischer Prozesse. Er erreichte dieses Ziel, indem er die Entropie S
mit der Zustandswahrscheinlichkeit W in Zusammenhang brachte, sodass die
Zunahme der Entropie in einem abgeschlossenen System einem Übergang von einem
weniger wahrscheinlichen in einen wahrscheinlicheren Zustand entspricht. Die
Formel, welche als Inbegriff des Lebenswerks Boltzmanns gilt, steht auch auf
seinem Ehrengrab im Wiener Zentralfriedhof. Sie heißt S = k · ln W, wobei k die
Boltzmann-Konstante ist. Boltzmann bildet den Ausgangspunkt der Quantentheorie
sowohl in der Formulierung, die Max Planck schon im Jahr 1900 gab, als auch in
der erweiterten Fassung, die von Albert Einstein aus dem Jahr 1905 stammt.
Andere bedeutende Leistungen Boltzmanns sind seine, aus statistischen
Erwägungen abgeleiteten, Verteilungsformeln für die Energie sich frei oder in
Kraftfeldern bewegender Atome (Maxwell-Boltzmann-Verteilung). Während eines
Aufenthaltes 1906 in Duino setzte er seinem Leben im Alter von 62 Jahren ein
Ende.
Ludwig Boltzmann wurde am 20. Februar 1844 in Wien
geboren. Er studierte Physik an der Universität Wien und war zwei Jahre
Assistent von Josef Stefan. 1869 wurde er Professor für mathematische Physik an
der Universität Graz. Das zentrale Problem seiner Arbeit war die Rückführung
der Thermodynamik auf die Mechanik und die dabei nötige Beseitigung des
Widerspruchs zwischen der Umkehrbarkeit mechanischer Vorgänge und der Einseitigkeit
thermodynamischer Prozesse. Er erreichte dieses Ziel, indem er die Entropie S
mit der Zustandswahrscheinlichkeit W in Zusammenhang brachte, sodass die
Zunahme der Entropie in einem abgeschlossenen System einem Übergang von einem
weniger wahrscheinlichen in einen wahrscheinlicheren Zustand entspricht. Die
Formel, welche als Inbegriff des Lebenswerks Boltzmanns gilt, steht auch auf
seinem Ehrengrab im Wiener Zentralfriedhof. Sie heißt S = k · ln W, wobei k die
Boltzmann-Konstante ist. Boltzmann bildet den Ausgangspunkt der Quantentheorie
sowohl in der Formulierung, die Max Planck schon im Jahr 1900 gab, als auch in
der erweiterten Fassung, die von Albert Einstein aus dem Jahr 1905 stammt.
Andere bedeutende Leistungen Boltzmanns sind seine, aus statistischen
Erwägungen abgeleiteten, Verteilungsformeln für die Energie sich frei oder in
Kraftfeldern bewegender Atome (Maxwell-Boltzmann-Verteilung). Während eines
Aufenthaltes 1906 in Duino setzte er seinem Leben im Alter von 62 Jahren ein
Ende. 
 Der
Spannungsmesser und das Thermometer sollten nah beieinander stehen, um sie
besser ablesen zu können.
Der
Spannungsmesser und das Thermometer sollten nah beieinander stehen, um sie
besser ablesen zu können. 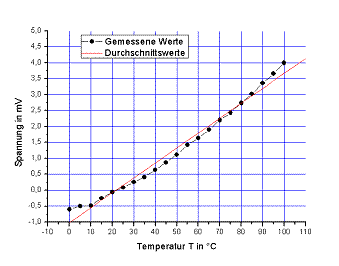


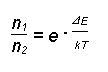
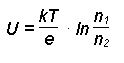
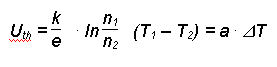
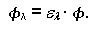 .
.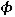 eines
schwarzen Strahlers ist als Funktion der Temperatur T und Wellenlänge
eines
schwarzen Strahlers ist als Funktion der Temperatur T und Wellenlänge 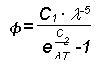
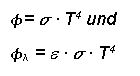 und
und 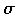
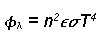 und
und 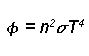 mit
n
mit
n 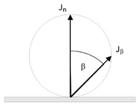 Laut
Lambert nimmt die Strahlungsstärke J
Laut
Lambert nimmt die Strahlungsstärke J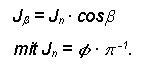
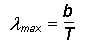
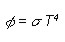
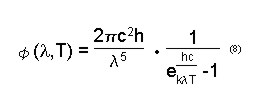
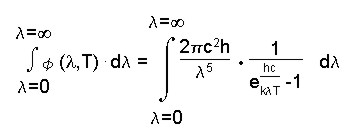
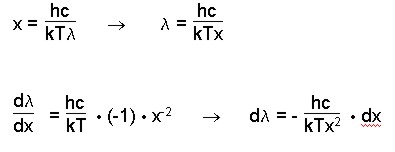
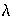
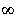
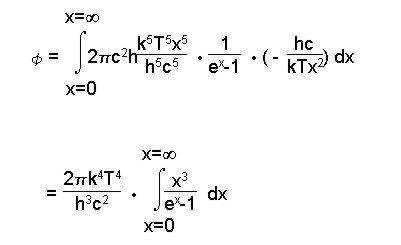
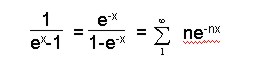
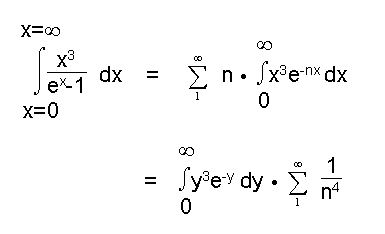
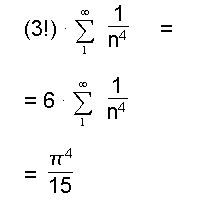
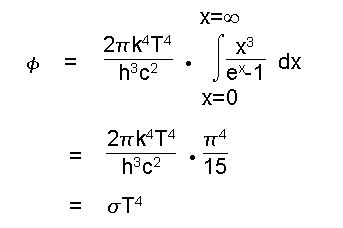
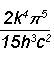 folglich die Stefan-Boltzmann Konstante
folglich die Stefan-Boltzmann Konstante
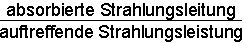
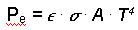 (A: Oberfläche)
(A: Oberfläche)